SEEM:

Understanding, Predicting and Better Resolving Q-Value Divergence in Offline-RL

Yang Yue*, Rui Lu*, Bingyi Kang*, Shiji Song, Gao Huang+,

  *Equal Contribution   +Corresponding author
▶ 1 Department of Automation, BNRist, Tsinghua University 2 Bytedance Inc.
arXiv Code Slide Poster

The Self-Excite Eigenvalue Measure (SEEM) offers a new theoretical framework and metric to understand, predict, and better resolve Q-value divergence in offline RL. SEEM can reliably predict upcoming divergence through the largest eigenvalue of a kernel matrix and accurately characterize the growth order of diverging Q-values. Finally, SEEM resolves divergence from a novel perspective, namely regularizing the neural network’s generalization behavior.

Abstract

The divergence of the Q-value estimation has been a prominent issue offline reinforcement learning (offline RL), where the agent has no access to real dynamics. Traditional beliefs attribute this instability to querying out-of-distribution actions when bootstrapping value targets. Though this issue can be alleviated with policy constraints or conservative Q estimation, a theoretical understanding of the underlying mechanism causing the divergence has been absent. In this work, we aim to thoroughly comprehend this mechanism and attain an improved solution. We first identify a fundamental pattern, self-excitation, as the primary cause of Q-value estimation divergence in offline RL. Then, we propose a novel Self-Excite Eigenvalue Measure (SEEM) metric based on Neural Tangent Kernel (NTK) to measure the evolving property of Q-network at training, which provides an intriguing explanation of the emergence of divergence. For the first time, our theory can reliably decide whether the training will diverge at an early stage, and even predict the order of the growth for the estimated Q-value, the model's norm, and the crashing step when an SGD optimizer is used. The experiments demonstrate perfect alignment with this theoretic analysis. Building on our insights, we propose to resolve divergence from a novel perspective, namely improving the model's architecture for better extrapolating behavior. Through extensive empirical studies, we identify LayerNorm as a good solution to effectively avoid divergence without introducing detrimental bias, leading to superior performance. Experimental results prove that it can still work in some most challenging settings, i.e. using only 1% transitions of the dataset, where all previous methods fail. Moreover, it can be easily plugged into modern offline RL methods and achieve SOTA results on many challenging tasks. We also give unique insights into its effectiveness.

SEEM Metric

In our paper, we theoretically prove that Q-value divergence happens when the maximal eigenvalue of the following matrix \(A_t\) (namely SEEM) is greater to 0:

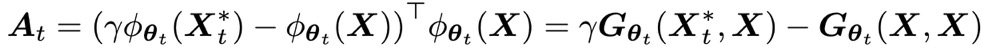
\(A_t\) is determined by a discount factor \(\gamma\) and the NTK between \(X\) and \(X^*_t\), where \(X\) is the vector composed of the state-action pairs \((s, a)\) in the offline dataset. \(X^*_t\) is the vector of the state-action pairs \((s^\prime, \pi_{\theta_t}(s^\prime))\) dependent on policy \( \pi_{\theta_t}\). The NTK matrix depicting the strength of the bond between \(X\) and \(X^\prime\) due to generalization is defined as \(G_{\theta_t}(X,X^\prime)=\phi_\theta(X)^T \phi_\theta(X^\prime)\), where \(\phi_\theta(X):=\nabla_\theta Q_\theta(X)\).

The intuitive interpretation for SEEM is as below: If SEEM is positive, the generalization bond between \(Q_\theta(X)\) and \(Q_\theta(X^*_t)\) is strong. When updating the value of \(Q_\theta(X)\) towards \(r+\gamma Q_\theta(X^*)\), due to strong generalization of the neural network, the Q-value iteration inadvertently makes \(Q_\theta(X^*)\) increase even more than the increment of \(Q_\theta(X)\). Consequently, the TD error \(r+\gamma Q_\theta(X^*) - Q_\theta(X)\) expands instead of reducing, due to the target value moving away faster than predicted value, which encourages the above procedure to repeat. This forms a positive feedback loop and causes self-excitation. Such mirage-like property causes the model’s parameter and its prediction value to diverge.

Prediction Ability

we can monitor SEEM value to know whether the training will diverge.

The divergence indication property of SEEM. The left figure shows the SEEM value with respect to different discount factors \(\gamma\). From the middle and right figures, we can see that the prediction Q-value (in blue) is stable until the normalized kernel matrix’s SEEM (in red) rises up to a large positive value, then we can observe the divergence of the model.

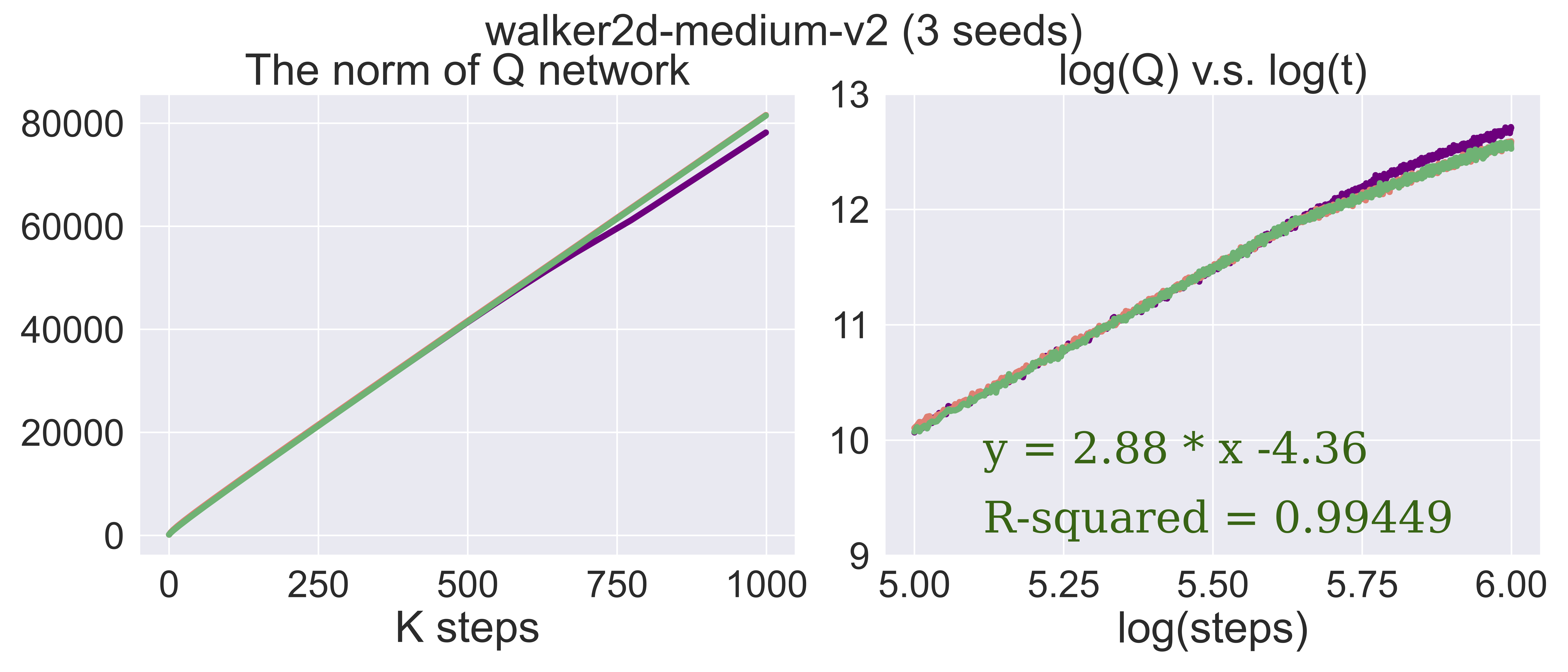
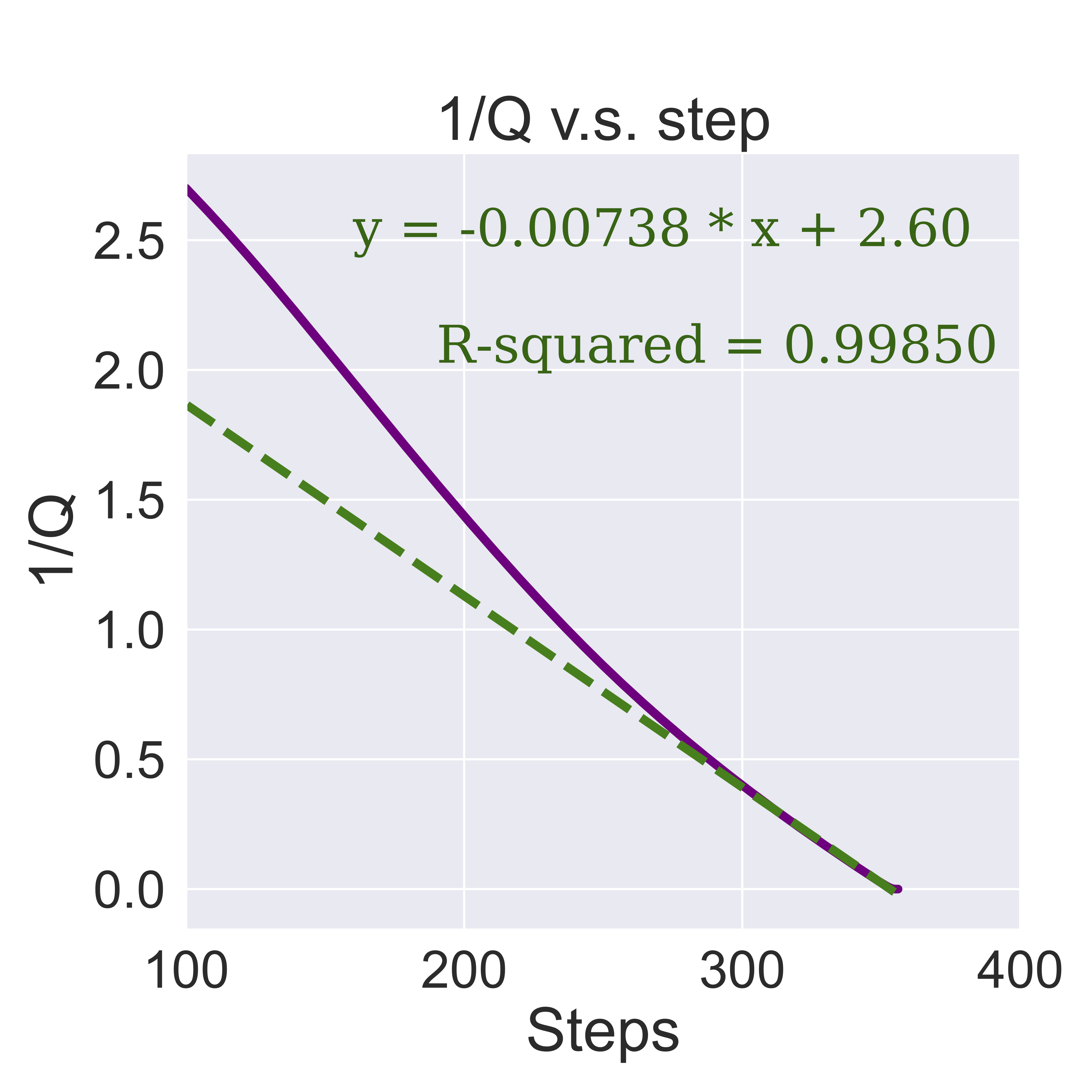
Except predicting whether the training will diverge, SEEM is able to predict the order of the growth for the estimated Q-value and the model's norm:

  • With Adam optimizer: The norm of the network parameters grows linearly and the predicted Q-value grows as a polynomial of degree \(L\) (the number of layers for Q-value network) along the time after a critical point.
  • With SGD optimizer: The inverse of Q-value decreases linearly along the timestep.
    • The Q-value growth prediction property of SEEM. The left and middle figure shows the case with the adam optimzer (\(L=3\)). The right figure showcases Q-value divergence with the SGD optimizer (\(L=2\)).

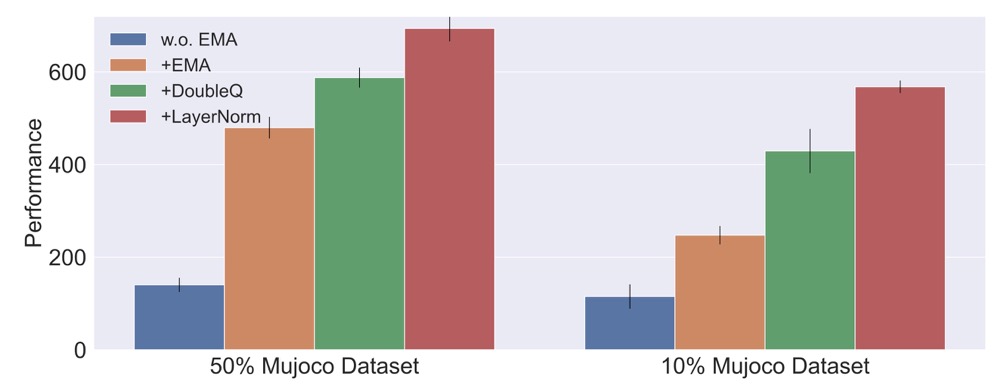
    Reducing SEEM By Normalization

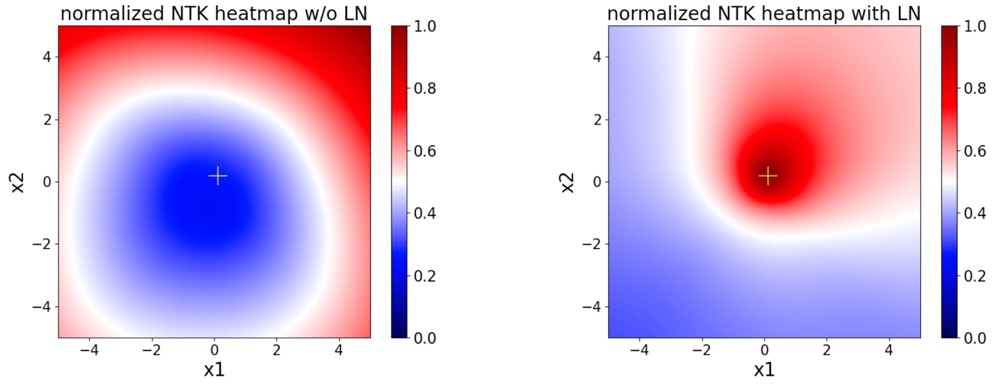
    In essence, a large SEEM value arises from the improper link between the dataset inputs and out-of-distribution data points. The MLP without normalization demonstrates abnormal behavior that the value predictions of the dataset sample and extreme points at the boundary have large NTK value and exhibit a strange but strong correlation. This indicates an intriguing yet relatively under-explored approach to avoid divergence: regularizing the model’s generalization on out-of-distribution predictions. Therefore, a simple method to accomplish this would be to insert a LayerNorm prior to each non-linear activation. We provide theoretical justification explaining why LayerNorm results in a lower SEEM value in the supplementary material of our paper.

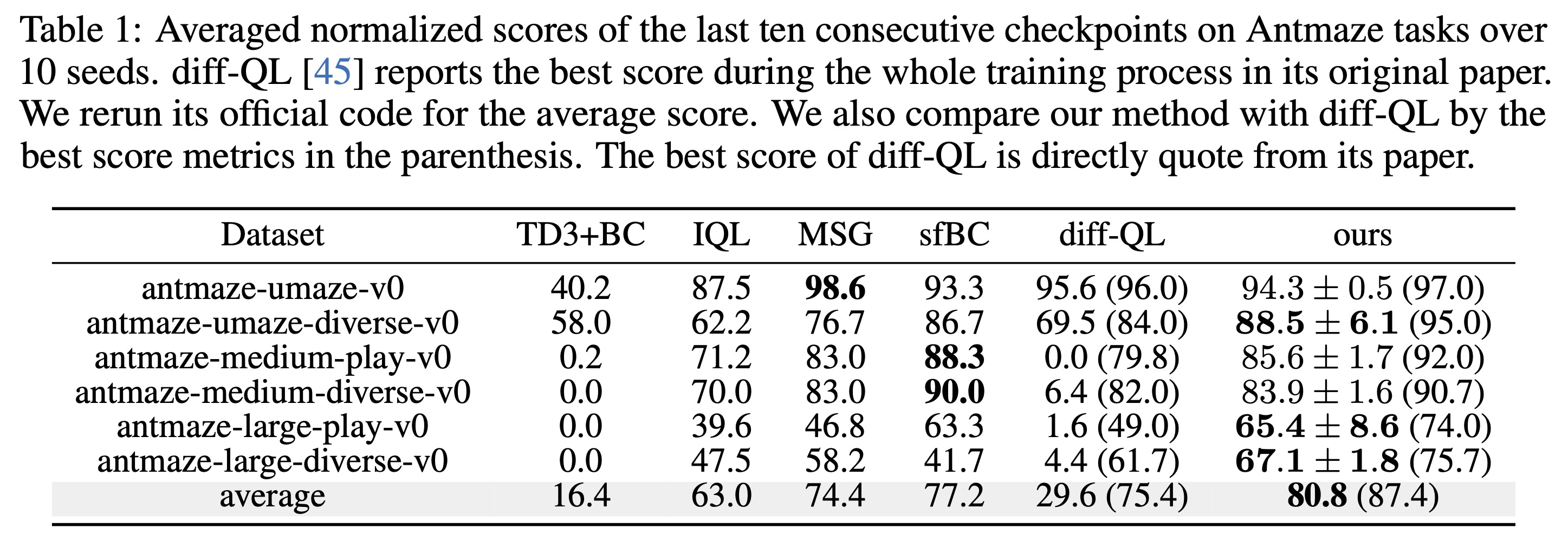
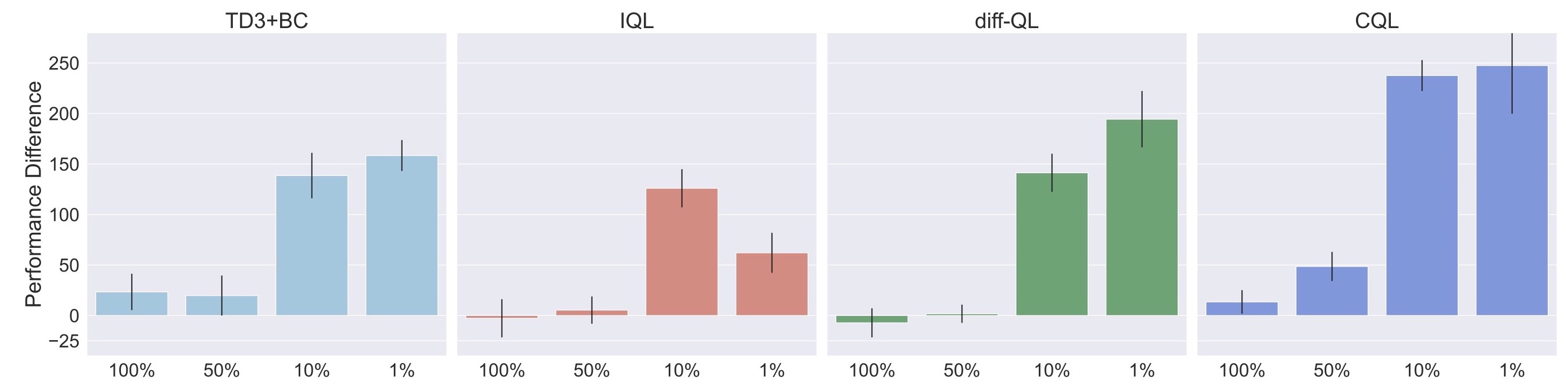
    The normalized NTK map for 2-layer ReLU MLP with and without LayerNorm.

    Agent Performance

  • Policy constraint (BC) is unable to control q-value divergence while performing well in some challenging environments. When the policy constraint is weak (BC 0.5), it initially achieves a decent score, but as the degree of off-policy increases, the value starts to diverge, and performance drops to zero. Conversely, when the policy constraint is too strong (BC 10), the learned policy cannot navigate out of the maze due to suboptimal data, and performance remains zero. In contrast, simply incorporating LayerNorm into Diff-QL, our method ensures stable value convergence under less restrictive policy constraints (BC 0.5). This results in consistently stable performance in the challenging Antmaze-large-play task.

  • Without full trajectories, Q-value divergence is more prone to happen. All popular offline RL algorithms reveal a marked drop when dataset is reduced to 10% or 1% (radnomly sampled transitions from D4RL datasets). We demonstrate the effectiveness of LayerNorm in improving the poor performance in X% datasets.

    • The performance difference between baseline with LayerNorm and without it using the same X% dataset.

    Ablate EMA, Double-Q, and LayerNorm on 10% and 50% Mujoco datasets.

  • Online RL Experiments - LayerNorm Allows Online Methods without EMA. It is natural to ask whether our analysis and solution are also applicable to online settings. Previous works has empirically or theoretically shown the effect of EMA in stabilizing Q-value and prevent divergence in online setting. To answer the question, We tested whether LayerNorm can replace EMA to prevent value divergence. Surprisingly, we discovered that LayerNorm solution allows the SAC without EMA to perform equivalently well as the SAC with EMA.

    • Conclusion and Future work

    In this paper, we propose an eigenvalue measure called SEEM to reliably detect and predict the divergence. Based on SEEM, we proposed an orthogonal perspective other than policy constraint to avoid divergence, by using LayerNorm to regularize the generalization of the MLP neural network. Moreover, the SEEM metric can serve as an indicator, guiding future works toward further engineering that may yield adjustments with even better performance than the simple LayerNorm. We hope that our work can provide a new perspective for the community to understand and resolve the divergence issue in offline RL. Anyone interested in this topic is welcome to discuss with us (yueyang22f at gmail dot com).

    BibTeX

    
@proceedings{yue2023understanding,
  title     ={Understanding, Predicting and Better Resolving Q-Value Divergence in Offline-RL}, 
  author    = {Yang Yue and Rui Lu and Bingyi Kang and Shiji Song and Gao Huang},
  booktitle = {NeurIPS},
  year      = {2023},
}